On the Thinking-Language Modeling Gap
in Large Language Models
"How does the language expression influence the reasoning process of LLMs?"
Language-Thought Modeling Gap
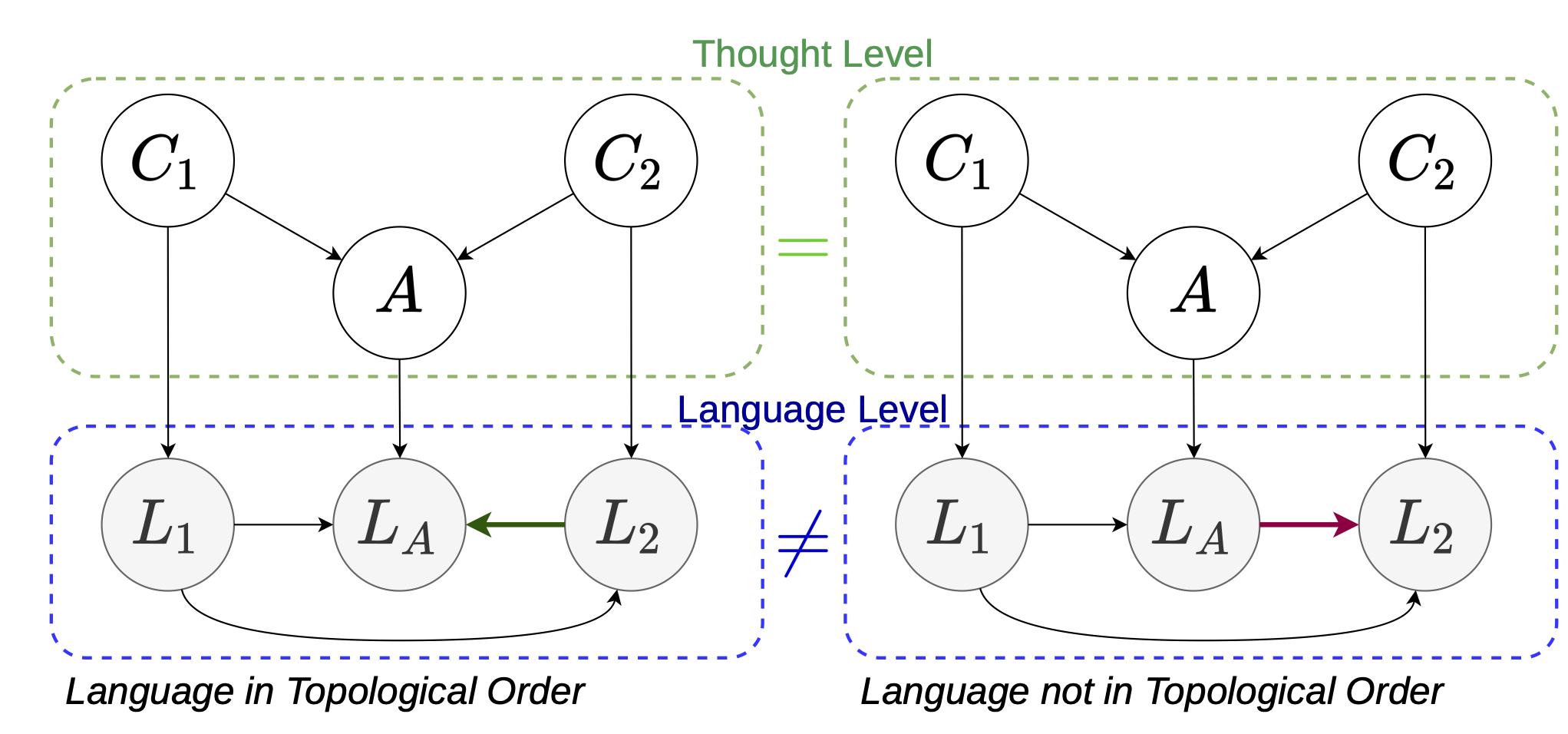
Running example: a two-premise question-answering (QA) setting. In the upper part, $C_1, C_2, A$ are latent random variables under a structural causal model: $C_1 \rightarrow A \leftarrow C_2$. In the bottom part, $L_1, L_2, L_A$ are tokens drawn from expression sets $\gL_{C_1=c_1}$, $\gL_{C_2=c_2}$, and $\gL_{A=a}$ respectively. There are two orders displayed in this figure: the left one is in the topological order of the underlaying causal graph, while the right one is not.
The Language-Thought Gap in LLMs' Reasoning
In this section, we first consider a simplified setting to demonstrate the problem, then we formalize our conjecture into two parts: language modeling bias for training phase; and language-thought gap for inference phase.
Formalization of the Data Generation Process
We consider thought as latent random variables and language as tokens to express the realized random variables. When random variable $X$ takes value $x$, one token from the token set $\gL_{X=x}$ would be written down. $\gL_{X=x}$ is defined as the expression for $X=x$.
Structural Causal Models
Suppose a set of latent variables $\mX = (X_1, \cdots, X_d) \sim P_{\mX}$. They follow a structural causal model specified by a directed acyclic causal graph $\gG = (\mX, \mE)$, where $\mE$ is the edge set. $\textbf{Pa}(X_i):=\{X_j \mid (j,i) \in \mE\}$ is the parent set. Each variable $X_i$ is defined by an assignment $X_i := f_i(\textbf{Pa}(X_i), N_i)$, where $\mN = (N_1, \cdots, N_d) \sim P_{\mN}$ are noise variables.
Running Example: Two-premise QA
Let $\mX = (C_1, C_2, A)$, and $\gG$ is $C_1 \rightarrow A \leftarrow C_2$. The token order $\pi$ has two possible choices, $(1,3,2)$ and $(1,2,3)$.
For each sample of $\mX = \vx$, a corresponding token sequence $\vl = (L_{\pi(1)}, \cdots, L_{\pi(d)})$ is generated, where $\pi$ represents the order of tokens. Each token $L_i \in \gL_{X_i = x_i}$ is selected from the expression set, and the distribution of $L_i$ is conditioned on the value of previous tokens up to $\mL_{i-1}$ and latent variables $\mX$, reflecting alternative linguistic expressions tailored to the context. The order $\pi$ is sampled from multiple candidates, imitating the flexibility in linguistic structures (grammar or syntax) in sentences.
How the Language-Thought Gap Influences the Reasoning Process
Despite the simplicity, two-premise QA generically models knowledge storage and extraction in LLMs, where $A$ can be considered as the knowledge to be stored and extracted. Essentially, two-premise QA can be easily generalized to various real-world downstream tasks. To resolve the two-premise QA, one needs to determine the values of the two premises. For humans, since the language order does not determine the language meaning when given proper conjunction words, one can easily change sentence structure as needed.
For example, one can use an order like $(C_1, C_2, A)$ or $(C_1, A, C_2)$ without affecting the underlying causal structures or the relations between $C_1$, $C_2$ and $A$:
As we'll see, this simple rewriting preserves the meaning but can fool an LLM in the training phase.
Training Phase
When the expression is not topological to the causal graph, e.g., the conclusion $A$'s causal parents $C_1, C_2$ are not all presented before itself, a language model with the next-token prediction objective tends to consider only the premise $C_1$ as the cause of $A$, instead of jointly considering both $C_1$ and $C_2$. In other words, language modeling based merely on the language can learn bias when the language presentation does not follow the topological order. Non-topological language can enforce a language model to learn a biased logic, which we term as biased reasoning:
Proposition: Language-Modeling Bias
When encountering the natural language sentence in an anti-topological order, e.g., $(C_1, A, C_2)$, language modeling with the next-token prediction objective will yield an LLM to draw the conclusion with incomplete information $C_1$, i.e., $\Psi( L_A \mid L_1)$ is fitting a marginal distribution:
Inference Phase
LLMs may not fully use a premise when it is expressed implicitly. The main intuition is that one piece of information can have different expressions in language. When a premise is expressed implicitly under a context, it's hard to notice and utilize for reasoning.
For example, two sentences, "Bob comes to the room" and "a man comes to the room", share gender information, but "Bob" emphasizes the name and expresses gender implicitly. Another example, in linear algebra, many statements have equivalences in different aspects, like conditions to be an eigenvalue or diagonalizability.
Consider a task to predict $A$ with $(C_1=c^*_1, C_2=c^*_2)$. The task is described by $(L_1, L_2)$ with $L_i \in \mathcal{L}_{C_i=c^*_i}$. The prediction is done by a language model with $\Psi(A|L_1, L_2)$. The loss is usually measured by their cross entropy, and is equivalent to the Kullback–Leibler divergence $\KL \big( \Pr (A|c^*_1, c^*_2) \big| \big| \Psi(A|L_1, L_2) \big)$.
Theorem: Language-Thought Gap
Under this setting, assuming perfect knowledge for simplicity, i.e., $\Psi ( A \mid C_1, C_2) = \Pr ( A \mid C_1, C_2) $, and assume Markov property for both distributions, i.e., $A$ is independent with others once $C_1,C_2$ are given. Then, it holds that:
where $\text{V}(p,q):=\sum_x |p(x) - q(x)|$ is the (non-normalized) variational distance between $p$ and $q$.
The variational distance term measures the cost of totally misunderstanding, while the term $\big(1-\Psi(c^*_1, c^*_2 \mid L_1, L_2) \big)^2$ measures how well the task is understood by the language model. The result means that even when the next-token predictor captures the correct relation between latent variables, it can exhibit biased reasoning with implicit expressions.
Discussion and Understanding
In the aforementioned analysis, we focus on the two-premise QA example to explain the hypothesis about the intermediate mechanism between written language and thought in mind. As shown by the Language-Modeling Bias proposition, the language model learns to give shortcut reasoning when information is not complete. By the Language-Thought Gap theorem, we show that even if all information is expressed in the context, the shortcut reasoning can be triggered when the expression cannot be understood well.
Verification: Prompt Intervention with Controlled Implicitness
In this section, we conduct experiments to support our hypothesis. The Kullback–Leibler divergence can be measured from accuracy, however, the question is how to measure $\Psi(c^*_1, c^*_2 | L_1, L_2)$. In practice, LLMs can only output the distribution for tokens, while $c^*_1$, $c^*_2$ are not. Therefore, we control the implicitness qualitatively by constructing a set of datasets where the information is either easy or hard to be understood.
The two types of implicitness
Whether the language is well understood can be represented in $\Psi(c^*_1, c^*_2 | L_1, L_2) = \Psi(c^*_1 | L_1) \cdot \Psi(c^*_2 | L_1, L_2)$. In general case, the conditional $\Psi(c_i | L_1, \cdots, L_{i-1}, L_i)$ is based on two parts: its own expression $L_i \in \mathcal{L}_{C_i=c^*_i}$; and its previous context $q_i := \{L_1, \cdots, L_{i-1}\}$. Therefore, it motivates the following two types of implicitness:
- L-explicitness: the local confusion when whether $\Psi(C_i=c^*_i | L_i)$ is small;
- q-explicitness: the global or contextual confusion when $\Psi(C_i=c^*_i | q_i, L_i)$ is small.
The Control of Implicitness
To verify our conjecture, we further construct the WinoControl datasets based on the original WinoBias dataset. It consists of sentences about the interaction between two entities with 40 different occupations under certain contexts.
For example, What does "she" refer to in The manager promoted the housekeeper because she appreciated the dedication?
The same sentence would occur twice with different genders. Two types of sentences are designed: for type 1, one must utilize the understanding of the context; for type 2, one can utilize the syntactic cues to avoid ambiguity. We take Type 1 sentences for evaluation because they are much more challenging.
In this task, $c_i$'s are the story context about two characters, while q's are other information like the gender-occupation inductive bias.
Control L-explicitness
The original sentence is already difficult. So we make the story easier to identify the correct character. Three levels are designed:
-
Add one sentence to exclude the wrong answer. In the previous example
The [housekeeper (wrong answer)] ate one [fruit] because [he (the different pronoun)] likes it.With this additional information, one can infer that "she" refers to "manager". -
Add one partially informative sentence to show that the correct answer is possible. For example:
The {manager (correct answer)} ate one {fruit} because {she (the same pronoun)} likes it.With this additional information, one can infer that "she" could refer to "manager". - Insert no sentence.
Control q-explicitness
To increase the q part, we add relevant but unhelpful sentences and mix them with other ones. We design three levels:
- Insert no sentence;
- We add two sentences with two different pronouns, with the template
The [occupation] ate one [fruit] because [he/she] likes it; - Repeat the procedure in level 1 for more such sentences.
Prompt-level Intervention Scheme
To further verify our hypothesis, we need to show the performance drop is due to the understanding of problem but not the reasoning ability. Therefore, we design prompt-level intervention that encourage LLMs to understand the given information. We design one intervention for each type of implicitness.
Echo Intervention for q-Implicitness
The key intuition is to encourage LLMs to figure out and focus on the key information that truly matters to the task. A prompt can be:
Expanding Intervention for L-Implicitness
The key intuition is to encourage LLMs to make attempt to draw new expressions from $\mathcal{L}_{C_i=c^*_i}$, and can have chance to find more explicit ones:
The Full Method
We propose the combined prompt-level intervention technique called Language of Thoughts (LoT). The theoretical motivation of LoT is to control both types of implicitness. The key idea is to decrease the $(1-\Psi(c^*_1, \cdots, c^*_i | L_1, \cdots, L_i))$ term. We evaluate two variants, LoT_1 and LoT_2 respectively, as follows:
Practical Usage
The method is designed to mitigate $(1-\Psi(c^*_1, \cdots, c^*_i | L_1, \cdots, L_i))$. The success of the whole task also depends on $\Psi(A | c^*_1, \cdots, c^*_i)$. Therefore, the method (highlighted part) is expected to be combined with reasoning methods like Chain-of-Thought.
Evaluation on the WinoControl Dataset
Empirical Setting
We test different prompt methods with gpt-4o-mini-2024-07-18.
For CoT method, it is Let's think step by step.
For LoT-series methods, we use Expand prompt and Echo prompt separately for verification. The others will be evaluated in next section.
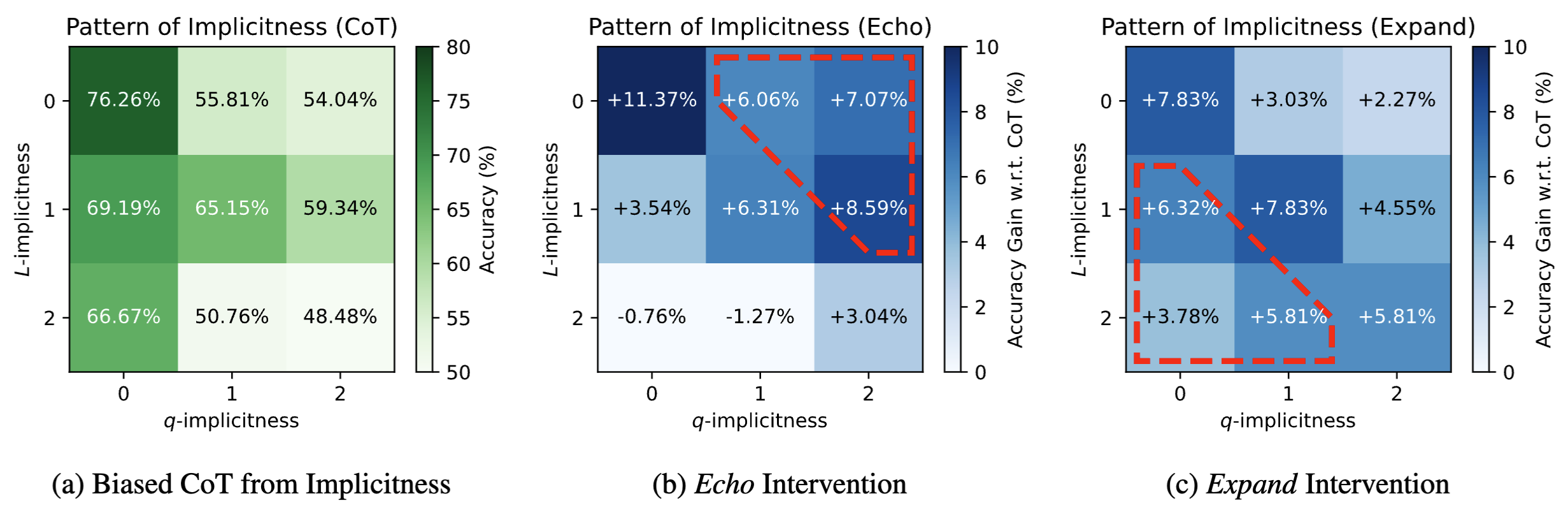
Is there a correlation between implicitness and performance?
As shown in the figure (a), the row and columns represent the level of L- and q- implicitness respectively. The accuracy of CoT would decrease with q- or L- level when the other one is fixed. In the upper-right corner, because we set L-level to zero by adding more helpful sentences, their effect can be slightly influenced when mixed with unhelpful ones. In general, the pattern is clear and consistent to our proposition.
Does each intervention helps to reduce the corresponding implicitness?
In the figure (b) and (c), we report and accuracy improvement under interventions w.r.t. CoT in (a). Comparing (b) and (c), as circled by red dashed lines, Echo has better performance than Expand in the upper right triangle, where q-implicitness is higher; Similarly, Expand is more effective in the bottom left when L-implicitness is higher. The patterns are consistent with our discussion.
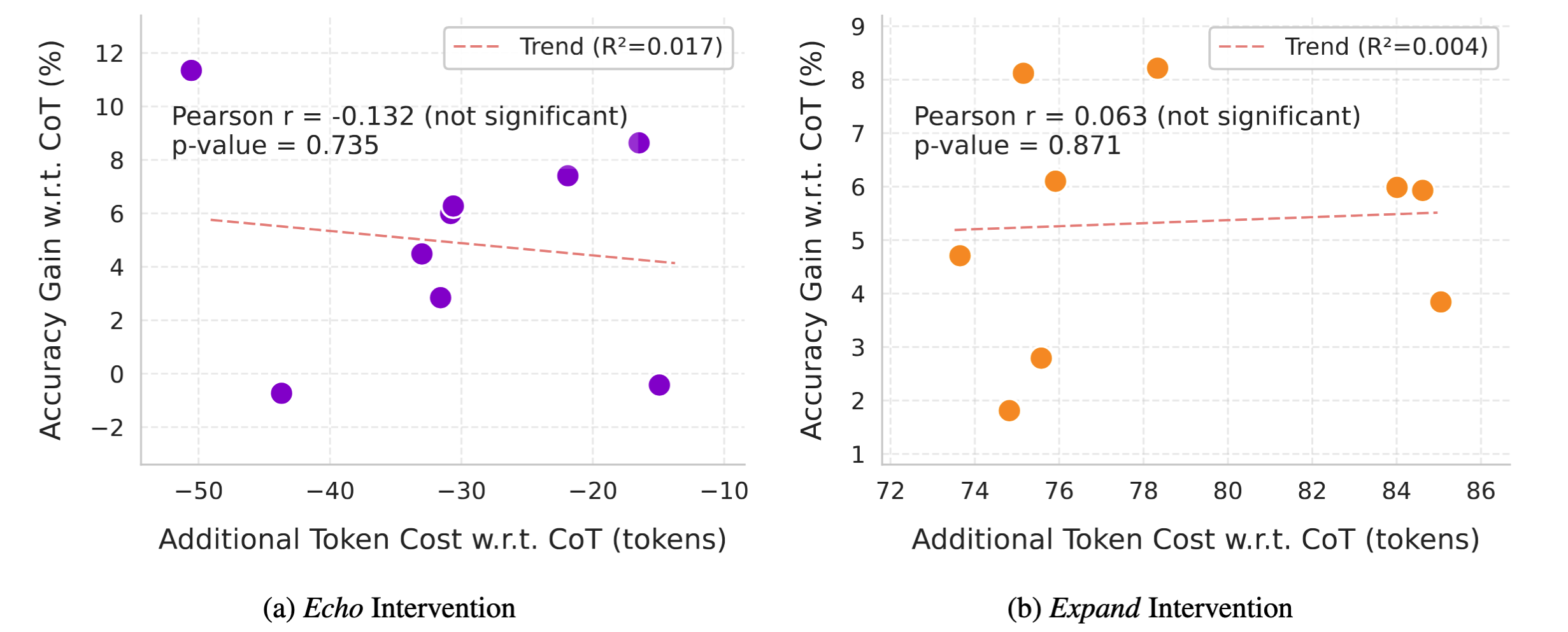
Is the improvements from more token cost?
In our token cost analysis figure, there is no significant correlation between interventions' improvement and additional token cost.
Interestingly, Echo costs fewer tokens and is better than CoT.
Comparison to related work
The observation in figure (a) is also consistent with literature on LLMs' failure mode. For example, the performance can be influenced by the order of premises in deductive tasks or by irrelevant context in math tasks. These failure modes can be explained by our proposition as they raised the $(1-\Psi(c^*_1, \cdots, c^*_i | L_1, \cdots, L_i))$ term in the lower bound. Our contribution is non-trivial given the formalization and understanding in earlier sections and detailed construction and interventions presented here.
Further Evaluation on Designed Benchmarks
In this section, we conduct further evaluation with 4 strong baselines by 4 widely-used LLMs in 1 math benchmark and 2 social bias benchmarks that are designed to test LLMs' specific abilities. The ablation study is done for each of them.
Evaluation Setting
For each benchmark, we evaluate two LoT variants, as well as the Echo and Expand interventions as ablation study. For baselines, we use CoT, RaR, and Least-to-Most (LtM) Prompting. We also construct RaR+CoT by combing RaR prompt with CoT in the same way as the four LoT series methods for more carefully controlled comparison. For LLMs, we use four well-known models: DeepSeek-V3, GPT-4o-mini, Qwen-2-72B-Instruct, and Llama-3.1-70B-Instruct-Trubo.
Results on WinoBias benchmark
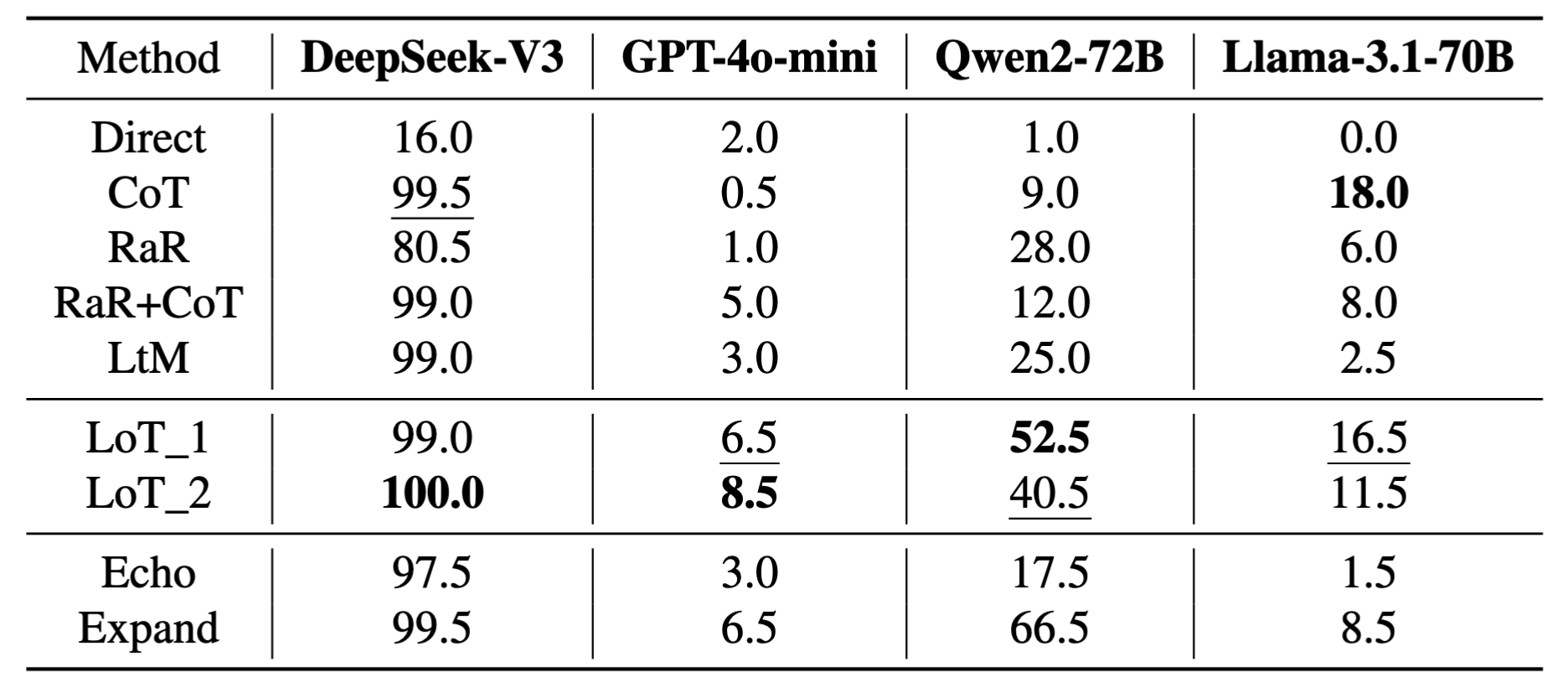
We use the original WinoBias dataset that has been introduced earlier. The main metric is the consistency (Con) between different pronouns. We also report the accuracy in each stereotype case (Anti and Pro), and their absolute difference (Delta).
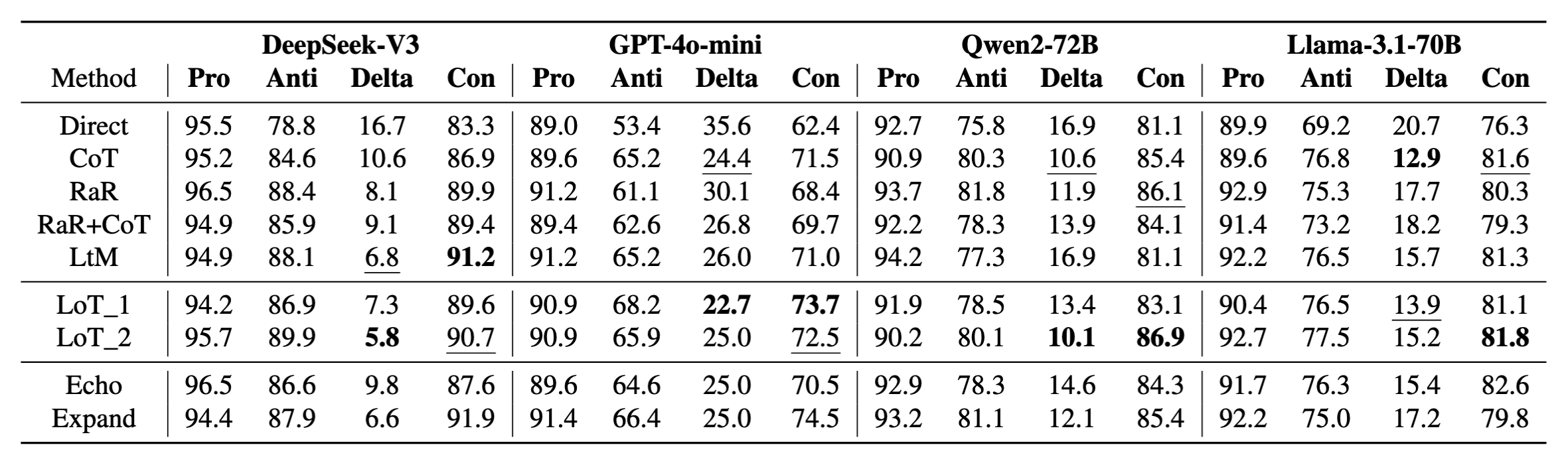
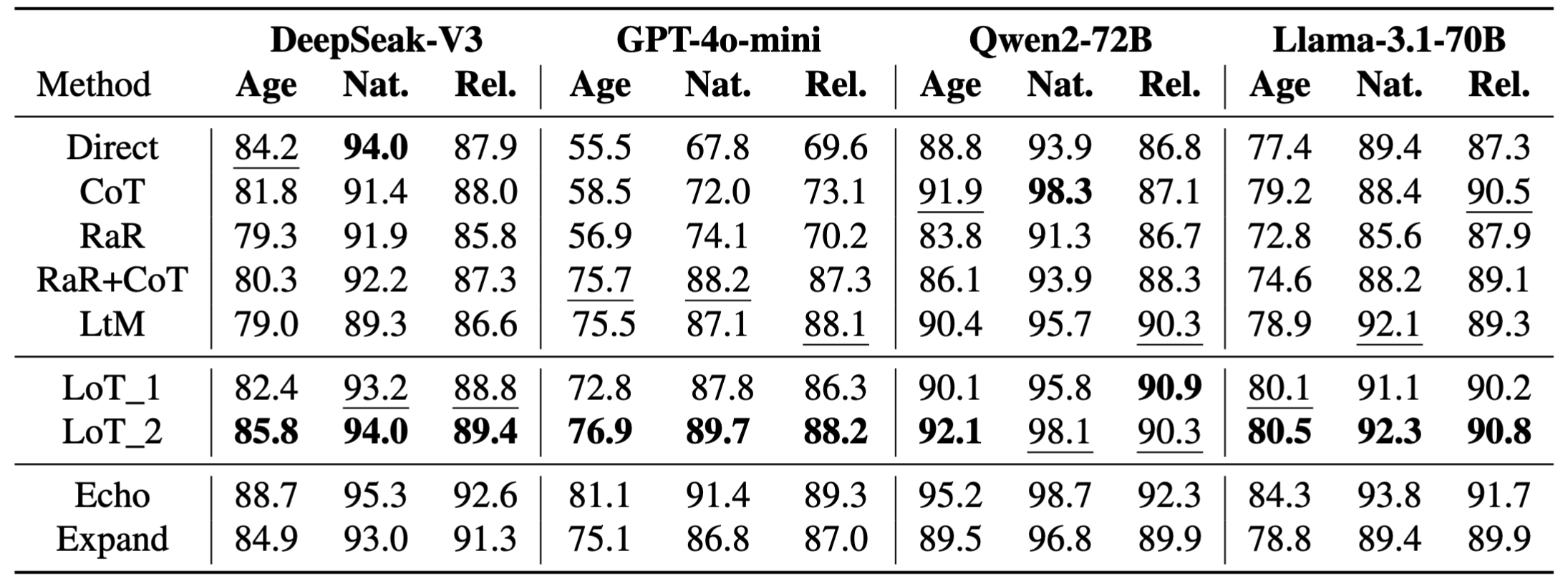
As shown in the table, RaR+CoT enhances the CoT method in DeepSeek. The two LoT methods get best or second-best performance in most cases. LoT_2 is slightly better than LoT_1. For ablation, one can observe that Expand is generally better than Echo and CoT, indicating the improvement is mainly on L-implicitness.
Evaluation on the BBQ benchmark
The BBQ benchmark consists of a set of question-answering problems. Each problem provides a specific context related to one typical stereotype. We use three bias types: Age, Nationality, and Religion, whose zero-shot direct-answering accuracy are worst, as shown by our pilot experiment.
Results show that Direct prompting is quite strong in DeepSeek-V3. RaR+CoT enhances the CoT method in the GPT model. LoT_2 obtains better performance than the five baselines in 11 out of 12 cases, and second best for Nationality Bias in Qwen model. LoT_1 is better than all five baselines in 3 cases and second best in 6 cases. For ablation, Echo is significantly better than Expand and CoT in all cases, indicating the strong q-implicitness.
Results on Alice benchmark
Alice Benchmark is a set of simple yet challenging math problems. The question is quite simple: Alice has N brothers and she also has M sisters. How many sisters does Alice's brother have?, and the correct answer is M+1 while the common wrong answer is M.
Following their template, we go through N, M∈[10] to get 100 questions. We then use another template Alice has M sisters and she also has N brothers for 200 ones in total.
In the results, all methods perform well in DeepSeek-V3. RaR+CoT enhances the CoT method in GPT and Qwen. LoT methods are second best for Llama and best for other two models, improving CoT by 8% in GPT-4o-mini and by 43.5% in Qwen. For variants, LoT_1 is better in half of the models. For ablation, Expand method is significantly better in all cases, indicating strong L-implicitness.
Case study and intuitive understanding
The two prompt-level interventions, Echo and Expand, can have failure cases, limited by the Language-Thought Gap. Here we discuss when they would succeed or fail, with examples from WinoBias and BBQ benchmark.
Echo, aiming to eliminate q-implicitness, can sometimes fail due to L-implicitness. In the WinoBias example, which has strong L-implicitness as we discussed above, it gives a statement "The mechanic then offered some books" which is misleading.
Similarly, Expand failed to capture the ill-post of question in the BBQ example, which has strong q-implicitness as we discussed above, and is misled to resort to additional assumptions.
When putting the two components together, they can be mutually beneficial. In the BBQ example, LoT also considered using "age bias", but is corrected by noticing the ill-post nature. In the WinoBias example, LoT first augments the content by "the mechanic is providing a service", then it states the "He then offered some books" correctly.
Experiments on General Reasoning Benchmarks
In this section, we extend our empirical studies with LoT to broader and more general reasoning tasks where CoT is shown to be limited and even underperform the direct prompting.
Experimental Setup
Benchmark We consider 8 challenging real-world reasoning tasks where CoT is shown to be limited when compared to direct prompting, including GPQA, FOLIO, CommonsenseQA(CSQA), MUSR, MUSIQUE, the AR split of the AGIEval-LSAT, the level 3 abductive and level 4 deductive reasoning from contexthub. The datasets cover from mathematical reasoning to soft reasoning. We do not include common mathematical benchmarks such GSM8k due to the potential data contamination issue and the results demonstrating the effectiveness of CoT in executing the mathematical calculation.
Evaluation To align with the evaluation in previous work, we do not adopt the DeepSeek-v3. Concretely, we benchmark LoT across 6 LLMs including GPT4o-mini, Llama-3.1-70B-Instruct-Turbo, Llama-3.1-8B-Instruct-Turbo, Mistral-7B-Instruct-v0.3, Claude-3-Haiku, and Qwen2-72B-Instruct.
We mainly consider two baselines as suggested by previous research. For the CoT results, we directly adopt the zero-shot Direct prompting and CoT responses provided by previous work. For a fair comparison, we do not directly incorporate the evaluation results while parsing the answers using the same parsing function, since the original evaluation results consider correct answers in the incorrect formats to be incorrect answers. We skip models without the responses provided such as Claude-3-Haiku in Abductive and Deductive reasoning. During the evaluation, some small LLMs or LLMs without sufficiently good instruction following capabilities may not be able to execute the instructions in LoT. Therefore, we use the bold out marker in markdown grammar to highlight the desired instructions. Empirically, it could alleviate the instruction following issue.
Experimental Results
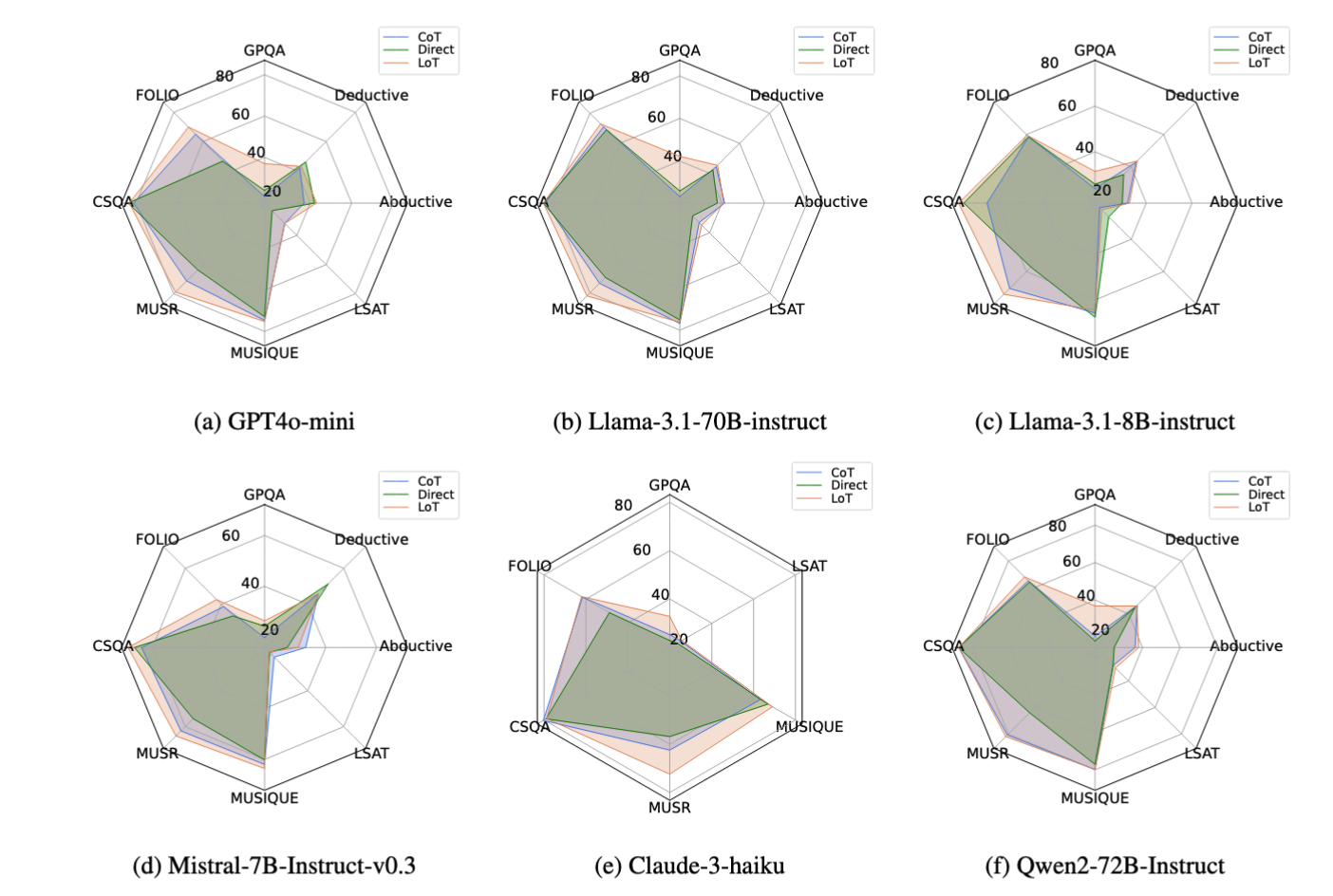
We present the results in Figure 3. It can be found that, for most of the cases, LoT brings consistent and significant improvements over CoT across various tasks and the LLMs up to 20% in GPQA, verifying the effectiveness of our aforementioned discussions. Especially in some reasoning tasks such as FOLIO, CoT underperforms Direct prompting, LoT is competitive or better.
Interestingly, LLMs with larger hyperparameters and better instruction-following capabilities usually have larger improvements. For example, the highest improvements are observed in Llama-3.1-70B and Qwen2-72B, while with Llama-3.1-8B and Mistral-7B, LoT does not always guarantee an improvement. We conjecture that small LLMs or LLMs with weaker instruction following capabilities may not be able to follow the LoT instructions.
Meanwhile, we also notice that there are some cases such as LSAT where LoT may not bring improvements or lead to minor performance decreases. We conjecture that merely using better prompts can not fully resolve the language-thought gap. On the contrary, the expansion prompt may exacerbate the language modeling biases as discussed before. Therefore, it calls for in-depth investigation and a better strategy that extends the idea of LoT to fully mitigate the language-thought gap such as developing better instruction tuning methods in the future work.
Contact
Welcome to check our paper for more details of the research work. For any question, please feel free to contact us.
If you find our paper and repo useful, please consider to cite:
will update once it is ready.